Using Keystroke Analytics to Improve Pass–Fail Classifiers
Kevin Casey
Maynooth University, Ireland
kevin.casey@nuim.ie
ABSTRACT. Learning analytics offers insights into student behaviour and the potential to detect poor performers before they fail exams. If the activity is primarily online (for example computer programming), a wealth of low-level data can be made available that allows unprecedented accuracy in predicting which students will pass or fail. In this paper, we present a classification system for early detection of poor performers based on student effort data, such as the complexity of the programs they write, and show how it can be improved by the use of low-level keystroke analytics.
Keywords: Learning analytics, keystroke analytics, data mining, virtual learning environments, student behaviour, early intervention
ISSN 1929-7750 (online). The Journal of Learning Analytics works under a Creative Commons License, Attribution - NonCommercial-NoDerivs 3.0 Unported (CC BY-NC-ND 3.0)
(2017). Using keystrokes analytics to improve pass-fail classifiers. Journal of Learning Analytics, 4(2), 189–211. http://dx.doi.org/10.18608/jla.2017.42.14
1 INTRODUCTION
High failure rates in undergraduate Computer Science courses are a common problem across the globe (Beaubouef & Mason, 2005; Biggers, Brauer, & Yilmaz, 2008). These poor progression rates, combined with the declining numbers of students enrolling in information and communications technology (ICT) programmes (Lang, McKay, & Lewis, 2007; Lister, 2008; Slonim, Scully, & McAllister, 2008) has led to a crisis for ICT companies looking for graduates. Estimates vary widely, but in the US for example, there were between 400,000 (Davis, 2011) and 1.25 million (Thibodeau, 2011) unfilled IT jobs in 2011, at a time when the US unemployment rate was running at 9%.
Against this backdrop, learning analytics (Siemens & Long, 2011) has become more widespread and has the potential to make significant contributions to understanding learner behaviour, with the caveat that high-quality, useful data is necessary. Education support systems such as virtual learning environments (VLEs) and learning management systems (LMSs) have the potential to generate the necessary data. This learner-produced data can then provide valuable insight into what is actually happening in the learning process, and suggest ways in which educators can make improvements; for example, identifying students at risk of dropping out or needing additional support in the learning process.
Accurate student performance prediction algorithms can provide the opportunity to determine when to intervene before a student reaches a level of performance that they cannot recover from. For these algorithms to be useful to the educator, they must be both accurate and timely (i.e., they must give accurate results early in the semester). However, the accuracy of such algorithms is based on the availability of data and, very often, sufficient data does not exist until late in the semester. This is a recurring problem with such algorithms in an early intervention scenario. If they are based solely on student effort in the course, then the predictions will be unreliable in the early stages of the semester. To improve reliability in these early stages, keystroke analysis was employed, specifically studying how students typed as they programmed. This approach has the advantage of yielding significant amounts of data early in the semester and has the potential to improve the timeliness of the classifier.
In this paper, the utility of keystroke analytics for performance prediction is evaluated. With accurate low-level keystroke timings for programmer activities, the following two research questions are addressed:
RQ1: Is there a correlation between certain types of keystroke metric and programmer performance?
RQ2: Can keystroke metrics be used to enhance the accuracy of pass–fail classifiers, particularly early in the semester?
The rest of this paper is organized as follows. In Section 2 (Prior Work), related work is discussed. In Section 3 (Dataset and Educational Context) the VLE, which yielded the data upon which the experimental work is based, is presented. This section also discusses the type of data collected and the software architecture of the system. Section 4 (Methodology) outlines the pass–fail classifier approach and how keystroke analytics are used. Section 5 (Results) presents the results from analysis. Section 6 (Discussion) examines how generalizable the results are, and discusses potential directions for future work. Section 7 (Conclusion) summarizes the results of the work.
2 PRIOR WORK
In the past few years, many universities have begun to focus on student retention. In computer programming, much effort has been put into changing the curriculum; for example, introducing pair programming (Teague & Roe, 2007) and problem-based learning (O’Kelly et al., 2004a; O’Kelly, Mooney, Bergin, Gaughran, & Ghent, 2004b). With the evolution of learning analytics, it has become possible to explore the effect of such curriculum changes, and student behaviour in general, at an unprecedented level of detail.
Casey and Gibson (2010) examined data from Moodle (one of the most widespread VLEs) for fifteen computer science modules in three different courses. The data stored in the system about the activities of both teachers and students is typically who performed the action, what action, when, and where. They found some interesting correlations that link with high performance, such as daily module logins, the amount of material reviewed, or Moodle usage over a weekend. In addition, they found extremely high student activity levels on Moodle for certain modules are sometimes a negative indicator for student performance. This negative correlation, which has been found in subsequent larger scale studies (Pardos, Bergner, Seaton, & Pritchard, 2013; Champaign et al., 2014) could be used to detect students with difficulties ahead of time, providing an excellent opportunity for early intervention.
Purdue University designed an early intervention solution for collegiate faculty entitled Course Signals (Arnold & Pistilli, 2012). Course Signals is a student success system that allows faculty to provide meaningful feedback to students based on predictive models, and to determine which students might be at risk. The solution helps to promote the integration between the student and the institution in different ways: faculty members send personalized mails to students regarding their performance in a given course and encourage students to join college activities. A predictive student success algorithm is run on demand by instructors. It has four components: performance, effort, prior academic history, and student characteristics.
Some researchers have highlighted cognitive overload as a potential cause for why learning programming is so difficult (Yousoof, Sapiyan, & Kamaluddin, 2007). Cognitive load provides a compelling argument as to why so many students fail to master it. The theory, although not without criticism, also provides pointers on how to address these problems. It is broadly accepted that an effective working memory is critical to academic performance (Yuan, Steedle, Shavelson, Alonzo, & Oppezzo, 2006). Limited to approximately seven items at a time, working memory is a short-term area of memory positioned between sensory memory and long-term memory (Miller, 1956). This area of memory is where cognitive processing takes place and is generally equated with consciousness.
Because cognitive processes occur in this area of memory, the two limitations, limited duration and limited capacity, can be seen as fundamental limitations of our cognitive processing ability. The capacity limitation can be overcome by schema formation — the grouping together of related items into a single item. These groupings can often be hierarchic in nature with lower-level groupings themselves being grouped together to form higher-level groupings.
As a result of this grouping (often called chunking), being asked to remember a sequence of letters such as [t,q,b,f,j,o,t] can be just as challenging to working memory as remembering a sequence of words (such as [the, quick, brown, fox, jumped, over, the]). This is despite the fact that there is much more information in the second list. In fact, if one were familiar with the phrase, then remembering the nineword list [the, quick, brown, fox, jumped, over, the, lazy, dog] would place a lower demand on one’s working memory than remembering seven arbitrary letters of the alphabet.
Given that chunking ability could play a significant role in a learner’s ability to master programming, it would be advantageous to measure it from the data available. For this, we turn to the area of keystroke dynamics — the study of patterns in a user’s typing. Keystroke dynamics has a number of application areas, from user authentication (Bergadano, Gunetti, & Picardi, 2003; Dowland & Furnell, 2004) to affective computing (Epp, Lippold, & Mandryk, 2011). Of particular interest in this paper is the use of keystroke dynamics to estimate a learner’s chunk recall times (Thomas, Karahasanovic, & Kennedy, 2005).
Central to the work of Thomas et al. (2005) is the notion of keystroke digraph latencies, the time taken for pairs of consecutive keystrokes. Specifically this is from the timestamp for the keydown event for the first keystroke to the timestamp for the keydown event for the second keystroke. By categorizing single keystrokes into five different categories and digraphs into three different categories (as seen in Table 1), the authors correlate digraph times with programming performance. Of particular interest are type-E digraphs, which are far more likely to occur at the beginning of a keyword and at the end of a keyword. These times coincide with when the learner is recalling the next token to type and so can be used as a measure for the learner’s chunk recall ability.
With reference to Table 1, consider the student typing the following line of code: MOV AL,BL. In Figure 1, the digraphs that arise can be seen.

Figure 1. Digraph construction.
In the example, there are three tokens (chunks). The first type-E digraph is composed of whatever character precedes the first “M” on the line (usually a newline character, marked by 1 in the example) and the “M” itself. The next type-E digraph is composed of the “V” and the subsequent space character. There follow four more type-E digraphs, the last being composed of the letter L and the subsequent character (usually a newline — marked by 2 in the example). In total, for the three tokens on the line of code, there are six type-E digraphs, two for each token.
Of all of the digraphs, type-E digraphs are of particular interest, because they measure the latency between keystrokes at the beginning and end of a token (or keyword). Other digraphs are less interesting from a cognitive load point of view. For example type-A digraphs, measure the latency between keystrokes in the middle of a keyword (essentially just giving a measure of typing speed), while type-H digraphs are typically associated with editing. It is only type-E digraphs that measure keystroke latency at the beginning and end of a token as the student types, and thus yields some information about how long it takes the student to decide upon or recall the next token.
Thomas et al. (2005) present a solid theoretical foundation for linking the type-E digraph measurements with cognitive performance. In two separate studies, one in Java, the other in Ada, they examine the correlation between the measured type-E digraph times and the student performance in related examinations. For this, they report Spearman correlations of –0.516 and –0.276 respectively. There were other differences in the studies to explain the results, such as programmer skill level and general experimental conditions.
A smaller scale study on predicting student performance from keystroke metrics was performed by Liu and Xu (2011). The study considered only keystroke frequency and not the type-E digraphs mentioned previously. The authors’ results were inconclusive. Indeed, they note that while many better coders type fast, some poor coders also exhibited a rapid keystroke frequency.
Longi et al. (2015) also use keystroke metrics so solve a slightly different problem, that of identifying a programmer from their keystroke timings. The authors used a number of approaches, with the most complex being to build a profile of the digraph timings for each programmer. A nearest neighbour classifier was then used to identify an unknown programmer by matching the digraph timings to the database of digraphs of known programmers. One of the more relevant findings is that, while a significant number of keystrokes are required for accurate classification, the typical student can accumulate the requisite number of keystrokes over just a couple of weeks of programming activity. Although the focus of Longi et al.’s paper is on programmer identification and not performance prediction, this finding hints that keystroke metrics could be a useful early indicator in a semester, yielding significant data after just a couple of weeks.
Other related research examines the role of writing speed in classification. Ochoa et al. (2013) report on successfully using handwriting speed (using a digital pen) to distinguish between experts and nonexperts in a collaborative environment solving mathematical problems. This work underlines the usefulness of such low-level features in solving classification problems.
An interesting project, similar in many ways to the VLE discussed in this paper, is the Blackbox project (Brown, Kölling, McCall, & Utting, 2014) where users of the popular BlueJ IDE can opt to contribute analytics on their programming. Brown et al. (2014) report that over one hundred thousand users have signed up. While the project has the potential to yield data on an unprecedented scale, the scale has forced the authors into the decision not to record low-level events such as mouse clicks and keystrokes because they would be too voluminous.
Romero-Zaldivar, Pardo, Burgos, and Kloos (2012) report on a successful trial examining the viability of virtual machines within a learning analytics context. The authors describe how they equipped each student in a second-year undergraduate engineering course with an instrumented virtual machine. This virtual machine recorded data as the students used it, and submitted it to a central server. While the analytics are also high-level, the authors do note that useful actionable information was obtained that could be fed back into the teaching process. Specifically, they were able to observe that hardly any students used a particular tool (the debugger) during the course.
Berland, Martin, Benton, Petrick Smith, and Davis (2013) discuss the importance of tinkering in the learning process. To measure it, they capture the various states of a program as a student edits it. The authors then analyze how students move though the state space of potential programs. While they found that different students took diverse paths, they were able to identify three phases to their learning. The result of their work is the EXTIRE framework, which characterizes the transitions that take place during tinkering. Other research concentrates on measuring the efficacy of tutoring software determining how robust learning is in an online tutor (Baker, Gowda, & Corbett, 2010, 2011), knowledge that can then be fed back into the instructional design process.
Ahadi, Lister, Haapala, and Vihavainen (2015) outline a promising classifier (based on decision trees) approach to predicting low-performing and high-performing programming students. Based on a number of features, the most effective being how the students performed on a subset of Java programming exercises they were given during the course. Using this approach, the authors report an accuracy of between 70% and 80%.
The sheer volume of data generated by learning analytics can be daunting. Scheffel et al. (2012) describe a method of data distillation, namely the extraction of key actions and key action sequences in order to leave behind meaningful data. The authors outline how the contextualized attention metadata (CAM) from a substantial university course in C programming is collected and then distilled using TF-IDF.
One notable feature of the VLE system presented in this paper is the potential for real-time analytics. Edwards (2013) notes that many systems such as GRUMPS as used by Thomas et al. (2005) do not operate in real time. Our VLE presented in Section 3, however, has the potential to operate in real-time with minimal work and, as such, has the potential to be a useful tool in the context of a laboratory session, where a tutor could intervene if a student was deemed to be struggling.
Finally, as the keystroke metrics discussed in this paper may allow the detection of cognitive overload for some students, it is worth considering how best to intervene or adapt teaching to cognitive overload. Yousoof et al. (2007) provide some guidance, arguing for the use of visualizations, in particular Concept Maps, to assist students suffering from cognitive overload. Garner (2002) suggests an approach of giving partially complete programs to students to reduce cognitive load. Caspersen and Bennedsen (2007) outline a cognitive load theory based foundation for an introductory programming course. It is also worth looking beyond research that seeks to address cognitive load. Other areas of research, such as the provision of enhanced error messages (Becker, 2015; Becker et al., 2016), do not directly deal with cognitive overload, but do have the potential to reduce the cognitive strain on the novice programmer. Additionally, a hints-based system can be employed to assist students. This has the added benefit of providing further information on student behaviour as the students use these hints (Feng, Heffernan, & Koedinger, 2006; Beal, Walles, Arroyo, & Woolf, 2007).
3 DATASET AND EDUCATIONAL CONTEXT
From 2012 to 2015 at Dublin City University, a new specialized platform for module delivery was developed and trialed for second year undergraduate computer science students on one of their core programming modules (Computer Architecture and Assembly Language Programming). This platform handled both module content and general learning activities within the module, all through a webbrowser (Figure 2). While content delivery is standard practice, easily handled by mainstream VLEs such as Moodle, the customized platform allowed for far more fine-grained analysis of how students consume material; for example, being able to determine how much time students are spending on individual lecture slides.
The second aspect of the platform — hosting general learning activities — is possible because the module is largely about programming. We have been able to move the tools that typically would have been used on the desktop into the browser itself, allowing students to program wherever they have a web-browser, with no need to install additional software. As students interact with the system, finegrained data on their interactions is recorded centrally with a view to improving the learning experience. The fact that so much day-to-day course activity is taking place on an instrumented platform allows for unprecedented opportunities in learning analytics and personalized content delivery.
Of course, because relevant student activity outside the platform cannot be measured, the question naturally arises as to how much student effort in the module is being captured by the platform. It is entirely plausible that students are, for example, reading lecture slides from a printout, an activity that we cannot measure. However, the slides that students view are HTML5-based and are not particularly easy to print. This combined with the data we have suggests that most students browse slides online. When it comes to measure coding effort, the only place students can compile and run their programs is within the platform. There is no alternative. Thus, we are more confident that the entirety of student effort in this regard is being captured.
3.1 Implementation Details
The VLE in question is implemented as a client-side Typescript/Javascript program. Students authenticate with the system using their campus login. The client-side application interacts with a CoreOS hosted server1 to retrieve learning materials such as course notes and weekly lab exercises. Usage data is collected by the Javascript client in JSON format, periodically compressed using a Javascript zlib library and posted to the server via a RESTful interface. To reduce load on the server, the data remains compressed until analysis is required. Keystroke data is only ever recorded for keystrokes inside the code editor window and is captured using Javascript keyboard events (onKeyUp, onKeyDown). This keystroke data is aggregated into blocks, each block beginning with a Unix timestamp and for each keystroke event, the key and the offset from that time is recorded.
The application simulates an 8-bit x86 microprocessor with a restricted amount of memory. Loosely based on Baur’s (2006) Microprocessor Simulator, a Microsoft Windows application, the simulator allows students to create small assembly programs, compile them, and execute them. As programs are executed, students can see a visual representation of CPU registers, memory, and a host of connected devices. Students can either run programs freely (adjusting their speed via slider) or can step through the programs instruction by instruction. Being browser-based, the application can be run in any OS with a reasonable web browser, though only Chromium browser was supported actively. Students could save their work and sessions on any computer, and resume sessions when they logged in elsewhere.
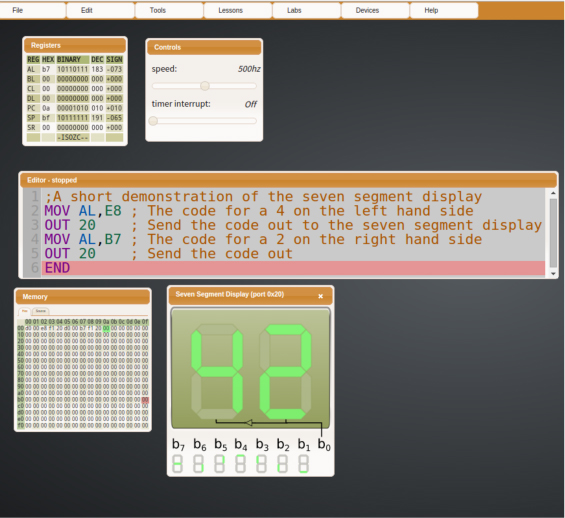
Figure 2: VLE for Assembly Language Programming.
Figure 2 shows some of the elements of the platform in action. The menu system can be seen across the top of the web page. Students can access different features of the simulator, view course notes, and submit work for grading from this menu. Shown on the screen, there are a few commonly used windows. On the top-left, a register status window can be seen. In this window, the current state of the various registers inside the virtual CPU can be seen. To the right of this is a configuration window where the speed of the CPU and the frequency of interrupts can be set. In the middle of the screen, the code editor window is shown. This is the window where students type their programs. At the bottom-left, a memory window shows the current state of memory in the virtual machine. Finally, on the bottom-right, a two-digit seven-segment display is shown. This is a good example of a virtual device that students can write programs to control.
Learning materials were integrated into the platform. A series of 20 lessons, identical to lecture slides, were made available in the platform. Students were encouraged to break away from the learning materials to try concepts out in the simulator, hence the tight coupling between the simulator and the learning material. Additionally, 8 lab exercises were also available. The labs and lessons were represented as HTML5 slides using the popular Reveal.js library (Ferreira, 2013). Although it was decided against it at the time, due to the experimental nature of the software, the learning materials could have been decoupled from the simulator and analytics collected on the server side via a Tin-Can API (Kelly & Thorn, 2013).
3.2 Module Structure and Grading
The module in question, Computer Architecture and Assembly Language, runs over a twelve-week semester. There are 36 hours of lectures with 24 hours of lab time. The learning outcomes are as follows:
LO1. Understand the operation of CPU registers
LO2. Describe how data is written to and read from memory
LO3. Calculate the numerical limits of memory and registers
LO4. Verify ALU operations by understanding the importance of the flags
LO5. Write 8086 Assembly Procedures
LO6. Design, Code, and Test Interrupt Driven 8086 Assembly programs
The module is delivered to 2nd year undergraduate computer science students in the first semester of the academic year. Continuous assessment accounts for 40% of the final grade while a final end of term exam accounts for 60% of the grade. The continuous component is broken up into two graded lab exams that take place on the platform. The final end of term exam is a written exam and covers a mixture of theory and practical coding. It is worth highlighting that when performance prediction is discussed in the context of this paper, it is the student performance in the final written exam and not the overall grade that is being predicted. This has the effect of eliminating the lab exams from the prediction and strengthens the results presented, in that the activity on the VLE is being used to predict the performance in an end-of-year written exam (and not a combination of a written exam and lab exams taken within the VLE).
3.3 Dataset
At the beginning of each semester that the module takes place, students are introduced to the platform. It is explained that all data can be removed at the end of semester on request (an opt-out policy). After a three-month waiting period following the end of the semester to allow for such requests, any remaining data is anonymized. For the 2013/2014 semester’s data upon which this work is based, data from 111 students remained after opt-outs (in this case none).
A substantial array of data was collected. Due to the volume of data, much of it was aggregated on the client-side and periodically sent to the server. Some of the data collected included: time spent on each slide of the learning materials, IP address, keystroke timings, successful compiles (recording a copy of the source code for each), failed compiles (again recording the source code) and GUI interactions such as menu clicks and window opening/closing.
To get a feel for the volume of data and the general pattern of activity on the platform, Figure 3 shows an activity diagram. This is the number of transactions observed from the students throughout the semester. Each line in the activity graph represents a single student. The data has been divided into discrete periods, representing the lab sessions and the time between those sessions. This concept has been added to the dimensions as activity during labs and outside labs. The total number of events extracted from the raw data for all students is 9,142,065, which together form a substantial digital footprint that represents student interaction with the system.
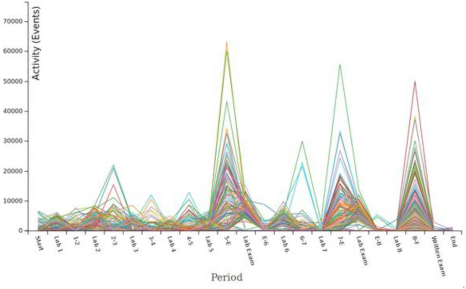
Figure 3: Student activity on a weekly basis.
As can be seen from Figure 3, the extent to which students on the module are assessment-driven becomes clear. There are three significant spikes in activity. These correspond to just before the first lab exam, the second lab exam, and the final written exam. For each of the two lab exams, a smaller spike in activity can be seen just to the right. This corresponds to the activity during the lab exam itself. While the observation of assessment-driven behaviour has previously been observed (Breslow et al., 2013), it is illuminating to see analytical data supporting the observation and highlighting the extent of the phenomenon for this particular module.
4 METHODOLOGY
4.1 Pass–Fail Classifier
We consider the prediction of a student’s performance in this course’s final written examination (pass/fail) given a number of important factors. The features or dimensions used for the prediction algorithm are simple features gathered from processing student interaction with the platform. The output of this prediction algorithm is whether a student fails or passes a course. The input to the prediction algorithm represents one or more observations regarding the student’s activity on the platform such as the number of successful and failed compilations, on-campus vs. off-campus connections, and time spent on the platform. The features used are presented in Table 2.
The complexity of the programs compiled was also measured and added to the dimensions vector. This metric has been calculated by removing the comments from each program compiled, running a compression algorithm and measuring the length of the compression for each program. This technique, examined in detail by Jbara and Feitelson (2014) is a useful proxy for code complexity.
The data listed in Table 2 contain attributes with a mixture of scales for different quantities. The machine learning methods used either expect or are more effective if the data attributes all have the same scale. The two scaling methods applied on the data were normalization and standardization.
In addition, the number of features or dimensions was reduced in order to verify whether feature reduction improves the prediction accuracy. Feature engineering, the judicious selection and preprocessing of such features, is one of the most challenging and important phases for such data-driven algorithms e.g., IBM Watson, Google Knowledge Graph (Anderson et al., 2013). To achieve this, the SelectKBest method from Scikit-learn was used in conjunction with the Chi-squared statistical test (Kramer, 2016, p. 49).
4.2 Classifier Options
Many different classifiers could be used for the prediction algorithm. Often the choice of which classifier to use is not clear, but there is a general paradigm for picking the appropriate classifier to obtain universal performance guarantees. Specifically, it is desired to select a function from the set of classifiers that has a small error probability. Effectively, the approach is to use training data to pick one of the functions from the set to be used as a classifier. Using this training data, the classifier with the minimum empirical error probability is selected.
The bag of classifiers used is composed of linear regression, a logistic regression, Gaussian naive Bayes, multinomial naive Bayes, Bernoulli naive Bayes, support vector machine with radial basis function kernel, K-neighbours (with K=12), and decision tree classifiers. To compare and evaluate different preprocessing techniques and models, a cross-validation approach was employed. For this particular study, a variant called “k-fold cross-validation” (Refaeilzadeh, Tang, & Liu, 2009) was used in order to compare the classifiers in the set.
The classifiers were all supplied by the Scikit-learn library embedded in a Jupyter/IPython notebook (Ragan-Kelley et al., 2014). Logged data was decompressed and preprocessed using a custom set of Python scripts and stored in a JSON format to be loaded later by the machine learning component written using Scikit-learn. As the decision tree classifier in Scikit-learn is the best performing one in later sections, it is worth noting that the Scikit implementation is an optimized version of CART (classification and regression trees; Breiman, Friedman, Olshen, & Stone, 1984), which is quite similar to C4.5 (Quinlan, 1996).
4.3 Utilizing Keystroke Data
To examine the viability of using keystroke metrics to improve the performance classifier, the timestamped keypress events were examined and the various digraph timings derived from them. Type-E digraphs discussed in Section 2 were the main focus here. During student activity on the platform, the keystroke timings were recorded within the code-editor window and stored on the server in a compressed form. Using a simple Python script, the average Type-E digraphs timing for each student was computed and then normalized within the test group. This was then used as the keystroke feature for the classification algorithm, updating with the new data for each week the classifier was run.
One of the issues faced with these digraphs was that of outliers. For example, during coding sessions, students are encouraged to interrupt their typing to sketch out ideas or to consult notes. Similar to the approach taken by Dowland and Furnell (2004) and Longi et al. (2015), a data pre-processing stage was applied to address these outliers. An upper bound of 2 seconds on the digraphs was applied, eliminating all digraphs with latencies greater than this. Once this threshold had been applied, a final step was taken of eliminating the bottom and top 10% outliers. To address the first research question, these type-E digraphs were considered in isolation first, ensuring a correlation with end-of-year exam performance. Then, these digraphs were used as additional feature in the pass–fail classifier to determine if they could enhance the accuracy of the classifier, in particular early in the semester.
5 RESULTS
5.1 Basic pass–fail classifier
The receiver operating characteristic (ROC), or ROC curve, is a graphical plot that illustrates the performance of a binary classifier system as its discrimination threshold is varied. In addition, leveraging a ROC area under the curve (ROC AUC) scoring function shows a reliable prediction accuracy score clearly greater than 69% for the decision tree classifier, doing an arithmetic mean for multiple crossvalidation folders. Figure 4 shows this classifier in action as the semester progresses.
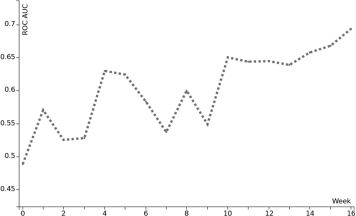
Figure 4: Prediction accuracy on a weekly basis.
Of note in Figure 4 is the way in which, as the semester progresses, the accuracy of the classifier improves. There are two related issues here. The first is that, naturally, the classifier improves as more data in the form of analytics from student activities arrives. The second is that student activity is generally back-loaded, in that they reserve most of their activity until just before the exam, so a significant amount of data is generated very late in the semester. This closely matches what is observed in the activity graph in Figure 3.
5.2 Linking Keystroke Metrics to Student Performance
In order to answer RQ1, it was necessary to correlate digraph measurements with student performance in the written exam. These digraph latency measurements are all based on the same set of 111 students over a 17-week period. There is a written examination at the end of this period and after this exam, the correlation between the type-E digraphs observed and the student examination performance was examined. Roughly in line with the observations of Thomas et al. (2005), peak correlation of –0.412 (with a p-value of 6.84x10-6) was observed.
In Table 3, the correlation between the digraph measurements observed up to a particular week and the students’ final written examination is presented. Traditionally, students are slow to sign up to the platform and this is evident from the table, with low correlation data in the first few weeks (and higher p-values). Consulting the logs, it became evident that it was not until the end of week 6 when the last student had started to use the platform.
What is particularly interesting about the correlation is that, although weak to moderate, it is relatively stable from week 6 until week 16. This is precisely the type of dimension required to improve the classifier. While the students in this course generally expend most of their effort in the last couple of weeks, there is more than enough activity on the system early on to establish their keystroke patterns that, in turn, have some predictive power as to how they will perform in the final written examination.
5.3 Extended pass–fail classifier
To answer RQ2 and evaluate the potential improvement that keystroke analytics can provide to the accuracy of the classifier, the basic classifier presented above was re-evaluated, this time adding the type-E digraph measurements to the pre-existing dimensions. For each week, the cumulative digraph measurements up to that point were used as the digraph dimension. The new results are shown in Figure 5.
It is clear that the addition of the type-E digraph latencies to the classifier improves prediction accuracy. Only in weeks 0, 3, and 5 does the original classifier do marginally better. As discussed earlier, this is not surprising since the full set of digraph latencies isn’t known until the end of week 6. Overall, the peak accuracy of the new classifier is 0.707 vs 0.693 for the old classifier.
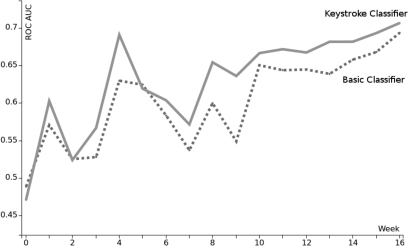
Figure 5: Improved prediction accuracy.
Although the improvement in the accuracy of the enhanced classifier is relatively small (0.014) at the end of the module, it does make a more significant difference overall early in the semester. The average week-by-week improvement through the entire semester is 0.028. The improvement in the classifier in earlier weeks is important to factor in, as reliable classification of non-performing students needs to take place as early as possible to allow enough time for interventions to be put in place. Figure 6 shows the confusion matrix for both classifiers at the end of the semester. The fractional values in the matrix arise due to the k-fold cross validation approach (the matrices shown represent an average of a number of matrices). As per Figure 5, the extended classifier shows an improvement over the basic classifier. To estimate the overall importance of the keystroke feature, the Gini Importance (Breiman & Cutler, 2008) of the features was computed. The most important features are shown in Table 4 where it can be seen that the average complexity of programs that the student writes remains the most important feature.
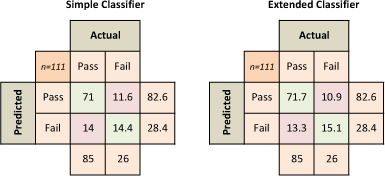
Figure 6. Confusion matrix for both classifiers after week 16.
6 DISCUSSION
While the approach taken to predict performance can be utilized elsewhere, it is worth noting how generalizable it is. The results presented are for one particular module, where low-level data from programming actions can be collected from a custom-built platform. While we are confident the results would extend to other programming languages, if the data were not collected, then obviously the same approach would not work. Therefore, careful attention would need to be paid to providing students with an appropriately instrumented platform if such low-level data is required.
The results can also be affected by the demographics involved. Those presented in this paper are from a reasonably homogenous group, namely 2nd year undergraduate computer science students with over 80% of the group being male. It is entirely possible that the predictive capability of the classifier could change with a different or more diverse demographic.
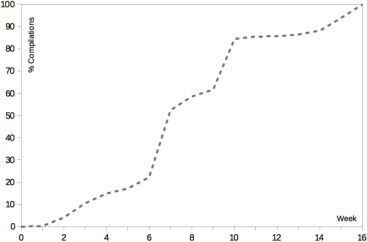
Figure 7: Cumulative program compiles over the module lifetime.
The most fundamental limitation of the approach taken in the platform is that only online activity can be measured. It is not possible to say anything about module-related activity that students perform offline, such as written exercises. Although unlikely in our case, if a student were handwriting programs during their studies, the current platform cannot capture this. A related issue is that, in order for the classifier to be accurate, there must be sufficient data available. For the module in question, students backload their work significantly. As can be seen in Figure 7, it is not until week 7 that students start to compile programs in significant amounts. At the end of week 6, only 22% of the final tally of compiled programs had been reached. By the end of week 7, this had reached 52%. Up until that point there is simply not enough data in the system to build a reliable classifier. On this basis, a reasonable time to intervene would be the midpoint of the 16 week period, just after week 8. Figure 8 shows the confusion matrix for the two classifiers at this point.
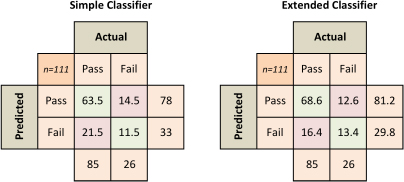
Figure 8: Confusion matrix for both classifiers after week 8.
There is room to improve the performance of the classifier further. To do this, we can utilize a number of strategies. One promising approach, given data that is currently available, is to examine the programs that students successfully write. It is possible to determine when a student employs a concept such as loops for the first time. The approach is particularly interesting from a pedagogical point of view as it is easier to link to course material and structure (as opposed to successful compilations or type-E digraph timings). Justification for investigating time-related features can be found in the behaviour of the classifier between weeks 4 to 7 (Figure 5), as the predictive power of the classifier actually diminishes. Preliminary investigations suggest that the classifier does quite well around week 4 since it is essentially recognizing early users of the system (and early users tend to correlate with better performers for this module). In subsequent weeks, additional data from later users of the system is included in the classifier features, thus “diluting” the capability of the classifier to spot early adopters. Thus, examining timerelated features and preventing this “dilution” has the potential to improve classifier performance considerably.
Including lab grades in the prediction can further enhance the predictive ability of the classifier. The type-E digraph timings used in this paper could also be refined. At present, all tokens (words in the programming language) are treated equally, but it may well be the case that some tokens are more difficult to recall. Applying different weightings to these may yield a more useful dimension for the performance classifier.
The best point at which to intervene is a complex topic, informed by classifier accuracy and also the specifics of the module being taught. Generally speaking, the best time to intervene is the time when the classifier can yield reasonable accuracy. More specifically, one should intervene as early as possible, once at-risk students have been identified accurately. For this particular module, this would be when sufficient data has been collected to ensure classifier accuracy. That would seem to be around week 7. Ideally, to allow even earlier identification of at-risk students, we should attempt to structure the learning so that students front-load their online work, allowing us to acquire the data that would identify at-risk students earlier. While we cannot recommend a particular week or point at which to intervene in general, this is the main recommendation to identify at-risk students early, and it is obvious in retrospect: get students using the online system as early and as intensively as possible.
7 CONCLUSION
Though the focus of this work is on showing that keystroke metrics can contribute to more accurate pass–fail classifiers, it is worth noting that the feature providing the greatest prediction accuracy was that of program complexity. This feature was obtained using a technique outlined by Jbara and Feitelson (2014) where the length of the compressed code was used as a proxy for the complexity of the code students write. However, this is merely an approximation for program complexity, so future work in improving this feature has the potential to yield substantial benefits.
While many other dimensions could be added to the classifier, keystroke digraphs are particularly interesting. Most importantly, they are relatively stable. Type-E digraph latencies do not vary hugely from the time they are first accurately measured. In contrast with other dimensions, such as the complexity of programs that students write (which naturally increases over time as students learn), it is an ideal early-indicator.
Not only being a good early indicator, digraph latencies also contribute something different than other dimensions that reflect effort expended by the student, such as time spent on the platform or programs compiled. Digraph latencies measure something intrinsic in the student abilities and, as such, are a valuable adjunct to these student-effort related dimensions.
There is also scope for improving the digraph latencies used. For example, a number of different options such as distinguishing between leading edge and trailing edge type-E digraphs were explored, but these did not contribute to classifier accuracy. Keystroke latencies were also adjusted to eliminate general typing speed as a factor, but again, these did not improve the accuracy of the classifier. Future work will explore these variations further.
It could be argued that the language used (an x86-like assembly) may also play a significant role in the predictive power of these digraphs. Typically there is a limited selection of short tokens in these assembly languages. Comparing the predictive power of digraph latencies of such a language with that of the latencies from a typical higher level language such as Java with more (and longer) tokens is desirable. Studies conducted by Thomas et al. (2005), where the authors investigated type-E digraphs for Java and Ada, show similar results. Thus, type-E digraphs are useful across multiple programming languages of varying syntactic structure and verbosity.
If such keystroke data is available, we have shown that it is worth incorporating keystroke analytics for improving the accuracy of such pass–fail classification systems. Improving this accuracy early in the semester, as keystroke analysis permits us to do, is critical to improving the opportunity for targeted intervention and, consequently, increased student retention.
REFERENCES
Ahadi, A., Lister, R., Haapala, H., & Vihavainen, A. (2015). Exploring machine learning methods to automatically identify students in need of assistance. Proceedings of the 11th Annual International Conference on International Computing Education Research (ICER ’15), 9–13 July 2015, Omaha, Nebraska, USA (pp. 121–130). New York: ACM. http://dx.doi.org/10.1145/2787622.2787717
Anderson, M. R., Antenucci, D., Bittorf, V., Burgess, M., Cafarella, M. J., Kumar, A., Niu, F., Park, Y., Ré, C., & Zhang, C. (2013). Brainwash: A data system for feature engineering. Proceedings of the 6th Biennial Conference on Innovative Data Systems Research (CIDR ’13) 6–9 January 2013, Asilomar, California, USA. http://www.cs.stanford.edu/people/chrismre/papers/mythical_man.pdf
Arnold, K. E., & Pistilli, M. D. (2012). Course Signals at Purdue: Using learning analytics to increase student success. Proceedings of the 2nd International Conference on Learning Analytics and Knowledge (LAK ʼ12), 29 April–2 May 2012, Vancouver, BC, Canada (pp. 267–270). New York: ACM. http://dx.doi.org/10.1145/2330601.2330666
Baker, R. S., Gowda, S., & Corbett, A. (2010). Automatically detecting a student’s preparation for future learning: Help use is key. In M. Pechenizkiy et al. (Eds.), Proceedings of the 4th Annual Conference on Educational Data Mining (EDM2011), 6–8 July 2011, Eindhoven, Netherlands (pp. 179–188). International Educational Data Mining Society.
Baker, R. S., Gowda, S. M., & Corbett, A. T. (2011). Towards predicting future transfer of learning. International Conference on Artificial Intelligence in Education (pp. 23–30). Lecture Notes in Computer Science vol. 6738. Springer Berlin Heidelberg. doi:10.1007/978-3-642-21869-9_6
Baur, N. (2006). Microprocessor simulator for students. Available at: http://tinyurl.com/5pyhnk
Beal, C. R., Walles, R., Arroyo, I., & Woolf, B. P. (2007). On-line tutoring for math achievement testing: A controlled evaluation. Journal of Interactive Online Learning, 6(1), 43–55.
Beaubouef, T., & Mason, J. (2005). Why the high attrition rate for computer science students: Some thoughts and observations. ACM SIGCSE Bulletin, 37(2), 103–106. http://dx.doi.org/10.1145/1083431.1083474
Becker, B. A. (2015). An exploration of the effects of enhanced compiler error messages for computer programming novices (Master’s dissertation). Dublin Institute of Technology.
Becker, B. A., Glanville, G., Iwashima, R., McDonnell, C., Goslin, K., & Mooney, C. (2016). Effective compiler error message enhancement for novice programming students. Computer Science Education 26(2), 148–175. http://dx.doi.org/10.1080/08993408.2016.1225464
Bergadano, F., Gunetti, D., & Picardi, C. (2003). Identity verification through dynamic keystroke analysis. Intelligent Data Analysis, 7(5), 469–496.
Berland, M., Martin, T., Benton, T., Petrick Smith, C., & Davis, D. (2013). Using learning analytics to understand the learning pathways of novice programmers. Journal of the Learning Sciences, 22(4), 564–599. http://dx.doi.org/10.1080/10508406.2013.836655
Biggers, M., Brauer, A., & Yilmaz, T. (2008). Student perceptions of computer science: A retention study comparing graduating seniors with CS leavers. ACM SIGCSE Bulletin, 40(1), 402–406.
Breiman, L., & Cutler, A. (2008). Random forests. http://www.stat.berkeley.edu/~breiman/RandomForests
Breiman, L., Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and regression trees (CART) Belmont, CA: Wadsworth International Group.
Breslow, L., Pritchard, D. E., DeBoer, J., Stump, G. S., Ho, A. D., & Seaton, D. T. (2013). Studying learning in the worldwide classroom: Research into edX’s first MOOC. Research & Practice in Assessment, 8, 13–25. http://www.rpajournal.com/dev/wp-content/uploads/2013/05/SF2.pdf
Brown, N. C. C., Kölling, M., McCall, D., & Utting, I. (2014). Blackbox: A large scale repository of novice programmers’ activity. Proceedings of the 45th ACM Technical Symposium on Computer Science Education (SIGCSE ’14), 5–8 March 2014, Atlanta, Georgia, USA (pp. 223–228). New York: ACM. http://dx.doi.or/10.1145/2538862.2538924
Casey, K., & Gibson, P. (2010). Mining Moodle to understand student behaviour. International Conference on Engaging Pedagogy (ICEP10), National University of Ireland Maynooth. Retrieved from http://www-public.tem-tsp.eu/~gibson/Research/Publications/E-Copies/ICEP10.pdf
Caspersen, M. E., & Bennedsen, J. (2007). Instructional design of a programming course: A learning theoretic approach. Proceedings of the 3rd International Workshop on Computing Education Research (ICER ’07), 15–16 September 2007, Atlanta, Georgia, USA (pp. 111–122). New York: ACM. http://dx.doi.org/10.1145/1288580.1288595
Champaign, J., Colvin, K. F., Liu, A., Fredericks, C., Seaton, D., & Pritchard, D. E. (2014). Correlating skill and improvement in 2 MOOCs with a student’s time on tasks. Proceedings of the 1st ACM Conference on Learning @ Scale (L@S 2014), 4–5 March 2014, Atlanta, Georgia, USA (pp. 11–20). New York: ACM. http://dx.doi.org/10.1145/2556325.2566250
Davis, J. (2011). CompTIA: 400K IT jobs unfilled. Channel Insider, 2 August 2011. http://tinyurl.com/ca699dr
Dowland, P. S., & Furnell, S. M. (2004). A long-term trial of keystroke profiling using digraph, trigraph and keyword latencies. IFIP International Information Security Conference (pp. 275–289). Springer US. http://dx.doi.org/10.1007/1-4020-8143-X_18
Edwards, S. (2013). Continuous Data-driven Learning Assessment. In Future Directions in Computing Education Summit White Papers (SC1186). Stanford, CA: Special Collections and University Archives, Stanford University Libraries. http://tinyurl.com/jep5vgt
Epp, C., Lippold, M., & Mandryk, R. L. (2011). Identifying emotional states using keystroke dynamics. Proceedings of the SIGCHI Conference on Human Factors in Computing Systems (CHI ʼ11), 7–12 May 2011, Vancouver, BC, Canada (pp. 715–724). New York: ACM. http://dx.doi.org/10.1145/1978942.1979046
Feng, M., Heffernan, N. T., & Koedinger, K. R. (2006). Predicting state test scores better with intelligent tutoring systems: Developing metrics to measure assistance required. In M. Ikeda, K. Ashlay, T.- W. Chan (Eds.), Proceedings of the 8th International Conference on Intelligent Tutoring Systems (ITS 2006), 26–30 June 2006, Jhongli, Taiwan (pp. 31–40). Springer Berlin Heidelberg.
Ferreira, D. (2013). Instant HTML5 Presentations How-to. Birmingham, UK: Packt Publishing.
Garner, S. (2002). Reducing the cognitive load on novice programmers. In P. Barker & S. Rebelsky (Eds.), Proceedings of the 14th World Conference on Educational Multimedia, Hypermedia & Telecommunications (ED-MEDIA 2002), 24–29 June 2002, Denver, Colorado, USA (pp. 578–583). Association for the Advancement of Computing in Education (AACE).
Jbara, A., & Feitelson, D. G. (2014). Quantification of code regularity using preprocessing and compression. http://www.cs.huji.ac.il/~feit/papers/RegMet14.pdf
Kelly, D., & Thorn, K. (2013, March). Should instructional designers care about the Tin Can API? eLearn Magazine. http://elearnmag.acm.org/archive.cfm?aid=2446579.
Kramer, O. (2016). Machine learning in evolution strategies (Vol. 20). Springer Berlin Heidelberg.
Lang, C., McKay, J., & Lewis, S. (2007). Seven factors that influence ICT student achievement. ACM SIGCSE Bulletin, 39(3), 221–225). http://dx.doi.org/10.1145/1268784.1268849
Lister, R. (2008). After the gold rush: Toward sustainable scholarship in computing. Proceedings of the 10th Conference on Australasian Computing Education (ACE ’08), Vol. 78, 1 January 2008, Wollongong, NSW, Australia (pp. 3–17). Darlinghurst, Australia: Australian Computer Society.
Liu, D., & Xu, S. (2011). An Empirical Study of Programming Performance Based on Keystroke Characteristics. Computer and Information Science, 2011 (pp. 59–72). Springer Berlin Heidelberg. http://dx.doi.org/10.1007/978-3-642-21378-6_5
Longi, K., Leinonen, J., Nygren, H., Salmi, J., Klami, A., & Vihavainen, A. (2015). Identification of programmers from typing patterns. Proceedings of the 15th Koli Calling International Conference on Computing Education Research (Koli Calling ’15), 19–22 November 2015, Koli, Finland (pp. 60–67), New York: ACM. http://dx.doi.org/10.1145/2828959.2828960
Miller, G. A. (1956). The magical number seven, plus or minus two: Some limits on our capacity for processing information. Psychological Review, 63(2), 81.
Ochoa, X., Chiluiza, K., Méndez, G., Luzardo, G., Guamán, B., & Castells, J. (2013). Expertise estimation based on simple multimodal features. Proceedings of the 15th ACM International Conference on Multimodal Interaction (ICMI ’13), 9–13 December 2013, Sydney, Australia (pp. 583–590). New York: ACM. http://dx.doi.org/10.1145/2522848.2533789
O’Kelly, J., Bergin, S., Dunne, S., Gaughran, P., Ghent, J., & Mooney, A. (2004a). Initial findings on the impact of an alternative approach to problem based learning in computer science. Proceedings of the PBL International Conference, Cancun, Mexico, June, 2004.
O’Kelly, J., Mooney, A., Bergin, S., Gaughran, P., & Ghent, J. (2004b). An overview of the integration of problem based learning into an existing computer science programming module. Proceedings of the PBL International Conference, Cancun, Mexico, June, 2004.
Pardos, Z., Bergner, Y., Seaton, D., & Pritchard, D. (2013, July). Adapting Bayesian knowledge tracing to a massive open online course in edx. In S. K. DʼMello et al. (Eds.), Proceedings of the 6th International Conference on Educational Data Mining (EDM2013), 6–9 July 2013, Memphis, TN, USA (pp. 137–144). International Educational Data Mining Society/Springer.
Quinlan, J. R. (1996). Bagging, boosting, and C4.5. Proceedings of the 13th National Conference on Artificial Intelligence (AAAI’96), 4–8 August 1996, Portland, Oregon, USA (Vol. 1, pp. 725–730). Palo Alto, CA: AAAI Press. http://dx.doi.org/10.1243/095440505X32274
Refaeilzadeh, P., Tang, L., & Liu, H. (2009). Cross-validation. Encyclopedia of Database Systems, pp. 532–538. Springer.
Ragan-Kelley, M., Perez, F., Granger, B., Kluyver, T., Ivanov, P., Frederic, J., & Bussonier, M. (2014). The Jupyter/IPython architecture: A unified view of computational research, from interactive exploration to communication and publication. American Geophysical Union, Fall Meeting Abstracts, #H44D-07 (Vol. 1, p. 7).
Romero-Zaldivar, V. A., Pardo, A., Burgos, D., & Kloos, C. D. (2012). Monitoring student progress using virtual appliances: A case study. Computers & Education, 58(4), 1058–1067. https://dx.doi.org/10.1016/j.compedu.2011.12.003
Scheffel, M., Niemann, K., Leony, D., Pardo, A., Schmitz, H. C., Wolpers, M., & Kloos, C. D. (2012). Key action extraction for learning analytics. Proceedings of the 7th European Conference on Technology Enhanced Learning (EC-TEL 2012), 18–21 September 2012, Saarbrücken, Germany (pp. 320–333). Springer Berlin Heidelberg. http://dx.doi.org/10.1007/978-3-642-33263-0_25
Siemens, G., & Long, P. (2011). Penetrating the fog: Analytics in learning and education. EDUCAUSE Review, 46(5), 30.
Slonim, J., Scully, S., & McAllister, M. (2008). Crossroads for Canadian CS enrollment. Communications of the ACM, 51(10), 66–70. http://dx.doi.org/10.1145/1400181.1400199
Teague, D., & Roe, P. (2007). Learning to program: Going pair-shaped. Innovation in Teaching and Learning in Information and Computer Sciences, 6(4), 4–22. http://dx.doi.org/10.11120/ital.2007.06040004
Thibodeau, P. (2011). Romney sees tech skills shortage: More H-1B visas needed. Computer World, 7 September 2011. http://tinyurl.com/76l4qxo
Thomas, R. C., Karahasanovic, A., & Kennedy, G. E. (2005). An investigation into keystroke latency metrics as an indicator of programming performance. Proceedings of the 7th Australasian Conference on Computing Education (ACE ’05), Vol. 42, January/February 2005, Newcastle, New South Wales, Australia (pp. 127–134). Darlinghurst, Australia: Australian Computer Society.
Yousoof, M., Sapiyan, M., & Kamaluddin, K. (2007). Measuring cognitive load: A solution to ease learning of programming. World Academy of Science, Engineering and Technology, 26, 216–219.
Yuan, K., Steedle, J., Shavelson, R., Alonzo, A., & Oppezzo, M. (2006). Working memory, fluid intelligence, and science learning. Educational Research Review, 1(2), 83–98. https://dx.doi.org/10.1016/j.edurev.2006.08.005
_________________________